Wärmespeicherfähigkeit

Was verbirgt sich hinter der Wärmespeicherfähigkeit der inneren Schichten, die im Tabreiter „Hitzeschutz“ angegeben wird? Bei einer Verdoppelung der Wandstärke erhöht sich die Wärmespeicherfähigkeit auf mehr als das Doppelte. Warum?

Der angezeigte Wert gibt an, wie viel Wärmeenergie notwendig ist, um die Raumtemperatur bei konstanter Außentemperatur um 1°C zu erhöhen. An diesem Wert sehen Sie schnell, ob Ihre Konstruktion mehr in Richtung Baracke (ca. 10kJ/m²K) oder oder Trutzburg (>500kJ/m²K) tendiert: Kleine Werte stehen für schnelles Aufheizen aber auch schnelles Auskühlen der Räume. Bei großen Werten ist eine sehr hohe Energiemenge notwendig, um den Raum aufzuheizen. Eine gute Konstruktion liegt in der Regel zwischen diesen beiden Extremen.

Da der Wert nur für konstante Außentemperatur gilt, ist er zur Beurteilung des sommerlichen Hitzeschutzes nicht geeignet.

Berechnungsverfahren

Bei der Berechnung dieses Wertes wird der Temperaturverlauf innerhalb der Konstruktion für zwei verschiedene Raumtemperaturen berechnet, die sich um 1°C unterscheiden, jeweils für den statischen Fall (t→∞). Mit Hilfe dieser beiden Kurven wird die mittlere Temperaturänderung dT für jede einzelne Schicht – und daraus die in der Schicht deponierte Wärmemenge berechnet.

dQ = dT * Dichte * spez.Wärmekapazität * Dicke.

Da die Außentemperatur festgehalten wird, ist die Temperaturerhöhung der innen liegenden Schichten am größten. Es tragen also hauptsächlich die inneren Schichten bei.

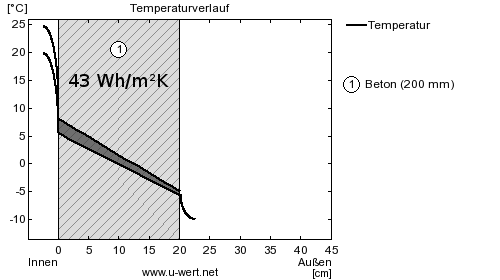
Dieser Sachverhalt lässt sich leicht grafisch veranschaulichen. In den folgenden Abbildungen sind die beiden Temperaturkurven eingezeichnet; um den Effekt deutlicher hervorzuheben für eine Temperaturdifferenz von 5°C. Die zwischen den beiden Kurven liegende Fläche entspricht der Wärmemenge, die für die Temperaturerhöhung notwendig ist (genau genommen entspricht dies dT*Schichtdicke und muss noch mit Dichte und spezifischer Wärmekapazität multipliziert werden, um die Wärmeenergie zu erhalten):

Deutlich zu sehen ist, wie die Temperaturerhöhung von innen nach außen abnimmt, und: Obwohl die Raumlufttemperatur um 5°C erhöht wurde, erhöht sich die innere Wandoberflächentemperatur nur um 2,5°C. Ursache ist der Wärmeübergangswiderstand, der für die Differenz Lufttemperatur-Oberflächentemperatur verantwortlich ist.

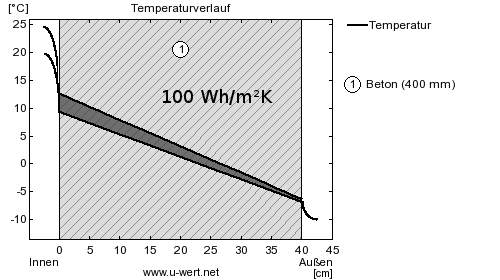
Verdoppelt man die Dicke des Betons, so spielt der Wärmeübergangswiderstand im Vergleich zum Beton eine geringere Rolle und die Temperaturdifferenz an der Wandoberfläche steigt auf 3,2°C. Deshalb steigt die Wärmespeicherfähigkeit von 43 Wh/m²K auf mehr als das Doppelte: 100 Wh/m²K.

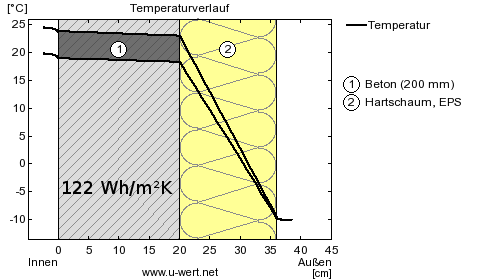
Eine außen liegende Dämmschicht bewirkt, dass fast die gesamte Temperaturdifferenz zwischen Raum- und Außenluft in der Wärmedämmung abfällt. Die Temperatur der gesamten Betonschicht entspricht in etwa der Raumtemperatur und macht deren Schwankungen fast vollständig mit. Im Ergebnis liegt die Speicherfähigkeit der 20cm dicken, gedämmten Betonwand deutlich über der 40cm dicken, ungedämmten Wand. Die Speicherfähigkeit der Dämmung selbst spielt in diesem Beispiel wegen ihrer wesentlich geringeren Dichte nur eine vernachlässigbare Rolle.

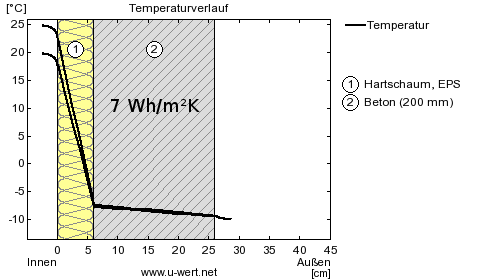
Eine Innendämmung bewirkt das genaue Gegenteil: Die Temperaturdifferenz fällt in der innersten Schicht ab, die Temperatur des Betons bleibt fast auf dem Niveau der Außentemperatur. Die Betonschicht nimmt kaum Wärmeenergie auf und entsprechend niedrig fällt die Wärmespeicherfähigkeit aus: Nur 7 Wh/m²K.